C. L'EFFICACITÉ D'UNE PÉRÉQUATION FONDEE SUR LA MODULATION DES PRÉLÈVEMENTS
Pour éviter que les communes les mieux dotées ne participent pas à l'effort de péréquation, on a modulé dans cette seconde simulation le taux de prélèvement sur les subventions implicites en fonction du revenu communal moyen au lieu de le maintenir constant . Il paraît équitable qu'une commune bénéficiant de peu de dégrèvements partiels, non en raison de la faiblesse de sa pression fiscale mais parce que ses habitants jouissent de revenus élevés, rende à la péréquation un plus fort pourcentage de ses subventions implicites qu'une commune où le revenu moyen est moins élevé.
La formule utilisée consiste à ne rien prélever dans les communes où le revenu est inférieur à la moitié du revenu moyen des villes de plus de 10.000 habitants et à faire croître asymptotiquement le taux du prélèvement vers le double du taux moyen retenu 65 ( * ) lorsqu'augmente le revenu communal.
La simulation effectuée en fonction de ce principe porte sur 970 millions de francs de prélèvements. Ces prélèvements ont ensuite été redistribués entre toutes les communes de plus de 10.000 habitants au prorata de l'indice synthétique des ressources et des charges.
1. L'efficacité globale du recyclage
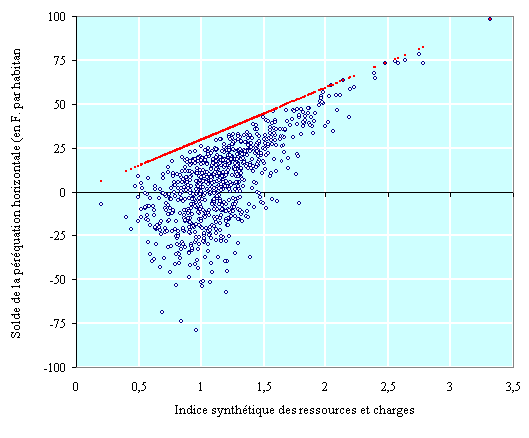
Cette efficacité globale se lit sur le graphique 4-11 (en se souvenant qu'une valeur élevée de l'indice synthétique sur l'axe des abscisses correspond à la situation des communes défavorisées par l'insuffisance de leurs ressources).Les transferts négatifs sont clairement concentrés autour d'une valeur de l'indice proche de 1, tandis que les transferts positifs se rapprochent de plus en plus de leur montant maximum (indiqué en rouge) lorsque la valeur de l'indice s'élève. Ceci résulte du fait que le taux de prélèvement sur les subventions implicites diminue dans les communes pauvres à indice de ressources élevé.
Graphique 4-9
Simulation d'une
péréquation horizontale en fonction d'un
prélèvement modulé sur les subventions implicites et d'une
redistribution basée sur l'indice de la DSU
2. L'impact de la péréquation horizontale sur les finances des grandes villes
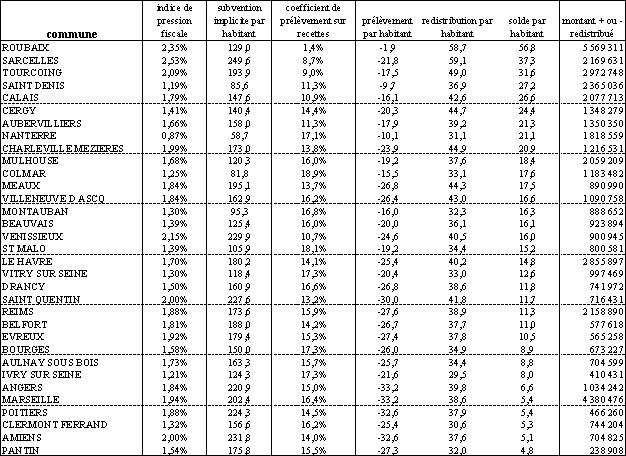
Un dernier tableau récapitule les principaux résultats obtenus pour l'ensemble des villes de plus de 50.000 habitants, classées suivant le solde redistribué par habitant, de Roubaix (+ 56,8 francs par habitant) à Cannes (- 68,9 francs par habitant 66 ( * ) . Ces montants peuvent paraître modestes mais ils correspondent à des montants absolus parfois considérables qui figurent dans la dernière colonne du tableau. Votre rapporteur spécial tient à cet égard à rappeler qu'il ne s'agit là que d'un exercice de simulation très ambitieux puisqu'il porte sur près d'un milliard de francs de transferts horizontaux et qu'il ne saurait être mis en oeuvre que très progressivement. Il souligne également que la redistribution opérée ne s'effectue pas uniquement entre les grandes villes figurant dans le tableau, dont beaucoup sont contributrices nettes, mais entre toutes les communes de plus de 10.000 habitants.
Les deux premières colonnes rappellent le taux moyen de pression fiscale dans la commune (exprimé par rapport au revenu médian et le montant par habitant des subventions implicites au titre des dégrèvements partiels
La troisième colonne fait apparaître l'impact du taux correcteur du prélèvement , par rapport à un taux moyen de prélèvement de 20 %. Des villes où le revenu moyen est élevé ont des taux de prélèvement qui peuvent atteindre 29 % (Paris) ou même 35 % (Neuilly) et descendre à 1,4 % à Roubaix ou 9 % à Tourcoing. Ce taux de prélèvement appliqué au montant des subventions implicites découlant des dégrèvements partiels fournit le prélèvement par habitant de la quatrième colonne. On constate que ce prélèvement peut être assez modeste, même avec un taux de prélèvement élevé, dès lors que le montant des dégrèvements et la pression fiscale sont faibles (par exemple à Versailles ou à Issy les Moulineaux).
La cinquième colonne indique le montant par habitant de la redistribution des ressources prélevées au prorata de l'indice synthétique des ressources et des charges de la DSU 67 ( * ) .
Enfin les deux dernières colonnes fournissent le solde péréquateur par habitant , c'est à dire la différence entre le prélèvement sur subventions implicites et la redistribution au prorata de l'indice de la DSU, et le montant correspondant en valeur absolue à imputer sur la DGF communale.
Tableau 4-3
Bilan de la simulation d'une
péréquation horizontale des subventions implicites entre les
villes de plus de 10.000 habitants
(données concernant l'échantillon des communes de plus de 50.000 habitants)
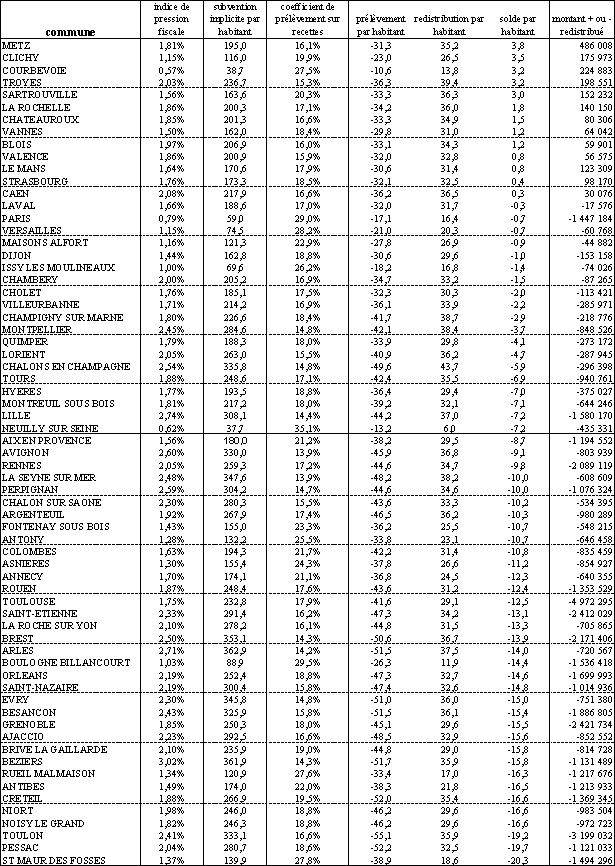
Bilan de la simulation d'une péréquation horizontale des subventions implicites entre les villes de plus de 10.000 habitants (suite)
(données concernant l'échantillon des communes de plus de 50.000 habitants)
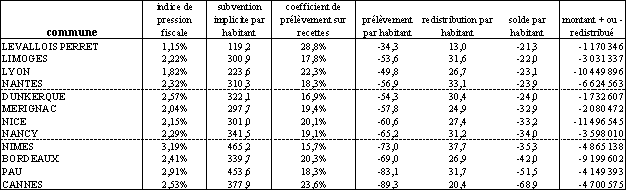
Bilan de la simulation d'une péréquation horizontale des subventions implicites entre les villes de plus de 10.000 habitants (suite)
(données concernant l'échantillon des communes de plus de 50.000 habitants)
* 65 Si r est le revenu moyen dans la commune et R le revenu moyen dans les villes de plus de 10000 habitants, le taux moyen de prélèvement est affecté dans la commune considérée d'un coefficient correcteur égal à 2 - (R/r). Si r = R, le coefficient correcteur est égal à 1. Si r < ou = 0,5R, le coefficient correcteur est égal à 0. Si r est très élevé, le coefficient correcteur tend vers 2.
* 66 Il s'agit comme dans le reste de ce rapport d'une donnée calculée en fonction de la population totale et non de la population DGF.
* 67 Avant application du coefficient multiplicateur et du coefficient d'effort fiscal.







