2. Rapprocher les critères d'éligibilité des critères de répartition
La dualité des critères d'éligibilité et des critères de répartition, ainsi que leur utilisation d'indicateurs différents 30 ( * ) , posent un problème de cohérence . De manière à rendre ces critères plus cohérents et à mieux équilibrer le dispositif, il serait opportun de rapprocher les critères relatifs à l'éligibilité de ceux permettant de calculer la répartition .
Les règles relatives à l'éligibilité, en particulier, pourraient ainsi mieux prendre en compte la réalité des territoires . Il pourrait donc s'agir d'identifier une méthode permettant de considérer, dès l'éligibilité au dispositif, un critère de superficie et/ou de densité , à l'image des règles de calcul utilisées pour la répartition.
Une piste consisterait à utiliser un critère de densité ou de superficie dès le calcul de l'éligibilité. Dans la mesure où le potentiel fiscal superficiaire permet, au sein des critères de répartition, de définir la moitié de la dotation de péréquation des régions, il serait légitime qu'il serve également dès le calcul de l'éligibilité.
Une autre piste, consisterait à prendre en compte les critères de charges liées à la densité . Cette orientation serait, en effet, particulièrement pertinente dans le cas des régions dans la mesure où l'on constate une relation statistique forte et assez continue entre la densité et les charges des collectivités régionales 31 ( * ) .
D'après les recherches de MM. Guy Gilbert et Alain Guengant 32 ( * ) , sur une période d'observation de 10 ans, les charges par habitant des régions décroissent avec l'augmentation de la population : les coûts semblent donc, pour les régions, inversement proportionnés à la densité, les économies d'échelle jouant à plein.
Le constat qu'ils dressent est le suivant : ces charges décroissent nettement en fonction de l'augmentation de la population dans les dix huit régions les moins peuplées et régressent également, mais plus légèrement, dans les autres régions plus peuplées comme l'illustre le graphique ci-après 33 ( * ) :
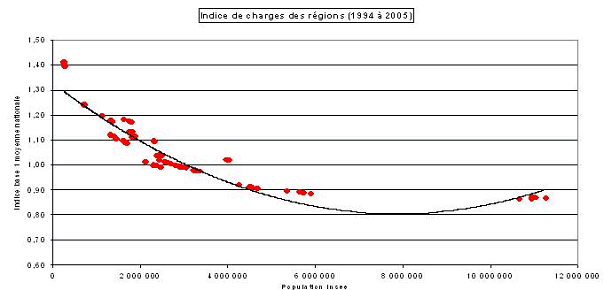
Source : présentation des travaux des professeurs Guy Gilbert et Alain Guengant devant le CFL le 28 octobre 2008
La légère remontée qui apparaît à droite dans la courbe 34 ( * ) ne doit pas remettre en question le principal enseignement de ce graphique : la corrélation statistique inverse entre les charges et le nombre d'habitants des régions . En effet, les points à droite du graphique, qui correspondent à l'Ile-de-France, sont situés plus bas que ceux de toutes les autres régions , y compris la région Rhône-Alpes, figurée par le premier groupe de points à la gauche de l'Ile-de-France, avec ses six millions d'habitants.
Ce constat , qui justifierait pleinement la prise en compte des critères de charges liées à la densité , ne vaut que pour les collectivités régionales .
En effet, l'observation statistique indique que la structure des charges n'est pas du tout corrélée à la population de la même façon pour les communes et les départements , dont les courbes de charges sont nettement en U.
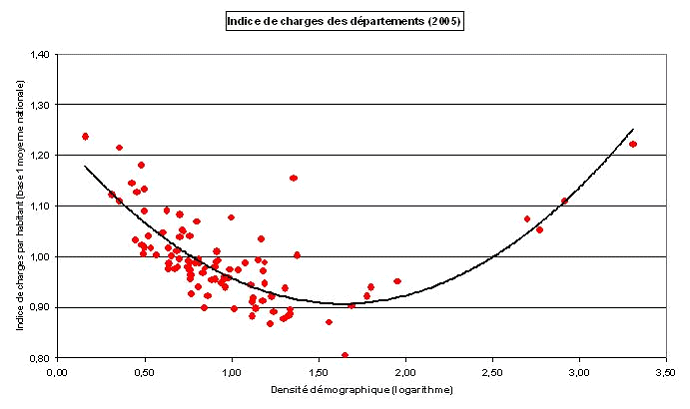
Source : présentation des travaux des professeurs Guy Gilbert et Alain Guengant devant le CFL le 28 octobre 2008
Pour les départements 35 ( * ) , les charges par habitant décroissent en fonction de la densité démographique dans les départements à faible densité (majoritaires) et s'accroissent nettement dans les départements les plus denses.
Dans le cas des communes 36 ( * ) , les économies d'échelle ne suivent pas non plus la même dynamique que celles des charges régionales.
En effet, les charges par habitant décroissent dans les communes jusqu'à un seuil compris entre 500 et 1.000 habitants puis augmentent au delà de ce seuil, dessinant, là aussi, une courbe en U .
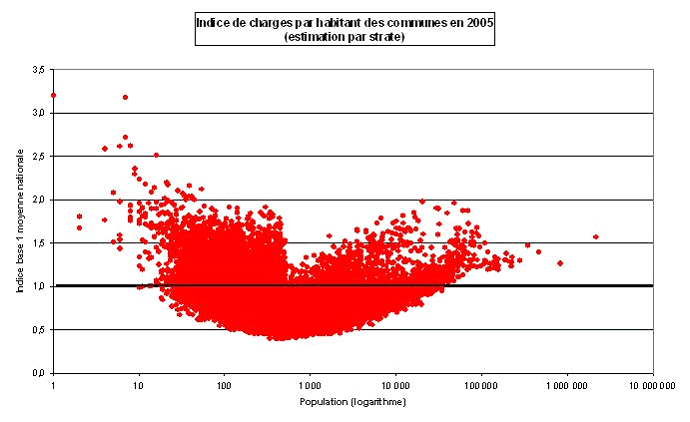
Source : présentation des travaux des professeurs Guy Gilbert et Alain Guengant devant le CFL le 28 octobre 2008
Ce constat empirique d'une augmentation des charges par habitant à partir d'une certaine taille des communes justifie le mode de calcul de la dotation de base des communes , composante de la dotation forfaitaire, elle-même intégrée dans la DGF communale.
Fonction croissante de la taille des communes, cette dotation de base est donc évaluée , conformément aux dispositions réglementaires 37 ( * ) , à l'aide d'un coefficient multiplicateur qui repose sur une fonction logarithmique .
Les charges des régions ayant à l'égard du nombre d'habitants une relation statistique inverse de celle des communes de taille intermédiaire et de grande taille, il pourrait être, par exemple, envisagé d'appliquer à la dotation de péréquation régionale une formule mathématique tirée de la corrélation constatée et fonctionnant donc à l'inverse de ce qui est déjà fait pour les communes.
Parmi les différentes modélisations mathématiques possibles permettant de traduire ce constat empirique dans un calcul opérationnel, votre rapporteur spécial en mentionne une, construite à partir des travaux de recherche des professeurs Guy Gilbert et Alain Guengant.
M. Alain Guengant a ainsi proposé à votre rapporteur spécial une formule tirant les conséquences de la baisse des charges par habitant en fonction de la population régionale . Votre rapporteur spécial présente, dans une annexe au présent rapport 38 ( * ) , les applications qu'il a pu faire de cette formule, qui repose sur une pondération de la population de chaque région dans le calcul du potentiel fiscal par habitant.
Cette modélisation mathématique présente l'intérêt de prendre en compte les charges liées à la densité , c'est à dire la population rapportée à la superficie, et donc de rendre plus cohérents les critères d'éligibilité et ceux relatifs à la répartition. Cette formule mathématique pourrait même inspirer de nouvelles règles de calcul de répartition de la dotation de péréquation, piste qui n'a pas été approfondie par votre rapporteur spécial, mais qui présenterait l'avantage d'unifier totalement les critères d'éligibilité et ceux relatifs à la répartition.
* 30 Pour mémoire, la première série de critères utilise uniquement un seuil de potentiel fiscal par habitant, tandis que l'autre ne repose qu'à moitié sur ce dernier et à moitié sur le potentiel fiscal superficiaire.
* 31 Votre rapporteur spécial souligne que le mode de calcul de ces charges ne peut, par définition, être totalement neutre et scientifique : un choix de méthode est nécéssaire quant aux charges retenues et à la façon de les pondérer entre elles. MM. Guy Gilbert et Alain Guengant utilisent, pour leur part, un indicateur synthétique de charges qui repose sur l'estimation statistique des charges à partir des dépenses des collectivités régionales.
* 32 Dans le cadre de la présentation précitée de leurs travaux devant le Comité des finances locales le 28 octobre 2008.
* 33 La présence d'un nombre de points supérieur à celui des régions s'explique par l'utilisation d'un panel statistique : chaque région est représentée par plusieurs points parce qu'elle apparaît au titre de plusieurs années. Lorsque les points se superposent, ce qui est souvent le cas en raison d'une stabilité des situations, le nombre précis de points n'est pas visible.
* 34 En effet, cette courbe de régression déduite du nuage de points correspond à la parabole d'ajustement par un polynôme du second degré. Toutefois, si l'on se contente de relier les points les uns aux autres, la baisse des charges, certes décroissante, est confirmée.
* 35 Le graphique réalisé pour les départements ne concerne qu'une seule année, tandis que le graphique consacré aux régions, à la page précédente, couvrait une période d'observation de dix ans. Votre rapporteur spécial appelle donc à la prudence dans la lecture de ces graphiques, particulièrement au niveau de leur comparaison. Il souligne également que cette réserve ne remet pas en question les principaux enseignements de ces études.
* 36 Le graphique consacré aux communes appelle la même précision méthodologique que pour les départements. Les données communales sont en effet elles-aussi annuelles.
* 37 Les coefficients ont été définis par le décret n° 2005-298 du 31 mars 2005 relatif aux dotations de l'Etat aux communes et aux départements. Par exemple, une commune dont la population est supérieure à 500 habitants et inférieure à 200 000 habitants se voit appliquée le coefficient suivant : a = 1 + 0,38431089 x log (population/500).
* 38 Cette simulation figure à l'annexe 6 du présent rapport.







