ANNEXES
Annexe 1 : Les stratégies défensives et offensives dans la négociation sur le temps de travail
Annexe 2 : Montant financier des mesures d'allégement du coût du travail pour l'emploi marchand
Annexe 3 : Temps partiel contraint ou choisi en France
Annexe 4 : Taux de marge des sociétés
Annexe 5 : Dispositifs ciblés et principaux destinataires
Annexe 6 : Historique des mesures
Annexe 7 : Annexes mathématiques
Annexe 1 : Les stratégies défensives
et offensives dans la négociation sur
le temps de travail
I. STRATEGIES DEFENSIVES
1. Réduction des salaires sans réduction du TT
|
Entreprise |
Obiectif emploi |
Modalités |
Evolution |
|
BORDELAISE DE CRÉDIT 790 salariés |
Préserver les emplois |
|
Après 18 mois les salariés ont récupéré leur salaire. |
2. Réduction des salaires avec réduction du TT
|
Entreprise |
salaires avec r Objectif emploi |
Modalités |
Evolution |
|
POTAIN 128 salariés non cadres concernés |
Garantir les emplois car sureffectif (crise de l'immobilier) |
Suite à le chute du CA :
|
9 mois après cet accord, la direction annonçait 58 licenciements Plus 13 cadres et 25 techniciens du SAV. |
3. Stratégies de temps partiel défensif
3.1. les entreprises industrielles
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|
SNECMA 13 000 salariés |
Réduction du nombre de poste de travail car évolutions constantes (économique, commercial, technologique) |
(aide FNE) avec incitation financière
an "compensation financière équivalente à 4 mois de salaire brut ou prêt pour formation |
1 an plus tard : un autre accord avec Mobilité géographique et professionnelle construite par une gestion individuelle des carrières (établie par la hiérarchie). |
|
GENERALE SUCRIERE 2 000 salariés |
Sauvegarder des emplois (baisse de consommation et concurrence forte) |
|
Entreprise en situation économique saine, mais déplacements des salarié d'un site à l'autre |
|
LU 535 salariés concernés |
Sauvegarder des emplois et résorber un sureffectif Faire face à un concurrence accrue |
|
77 suppressions d'emplois en décembre 94 |
|
DISCO 500 salariés |
Sauvegarder des emplois |
Convention avec pouvoirs publics pour temps partiel à mi-temps Prime exceptionnelle mensuelle Abonnement retraite S.S. et retraite complémentaire PRP avec prime exceptionnelle au moment du passage Aides financières à la mobilité géographique |
3.2. des entreprises de services
|
BRED 2 250 salariés |
Maintien des emplois |
Afin de réduire les frais de personnel, Pour 1'ensemble du personnel
Et pour le personnel administratif
|
1 an plus tard. 100 administratifs (en sureffectif) ont été réorientés dans des fonctions de commerciaux. |
|
IBM France 15 000 salariés |
Maintien des emplois et création d'un nouveau modèle d'entreprise |
Temps partiel à la carte :
|
Relance du dialogue entre employés et hiérarchie. Aucun conflit et adhésions de plus en plus nombreuses au temps partiel à la carte. |
|
PARIBAS 3 500 salariés |
Adaptation de l'organisation au temps partiel |
- Temps partiel aidé : incitation financière sans réduction des droits à la retraite
|
Temps partiel annualisé : 25 personnes dont 1/3 d'hommes Temps partiel aidé : 38 personnes. |
II. STRATEGIES OFFENSIVES
1. stratégie offensive de RTT
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|||
|
AFER 100 salariés |
|
|
|
|||
2. stratégies offensives privilégiant l'aménagement du TT (durée d'utilisation des équipements
2.1. les entreprises industrielles
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|
FONDERIE BOUHYER 230 salariés concernés |
Aménagement durée du temps de travail et travail en équipes |
|
|
|
HEWLETT-PACKARD FRANCE 200 salariés concernés |
Flexibilité des horaires de travail en équipes |
possibles) avec horaire moyen de 35 h
|
37 postes crées |
|
KODAK-PATHE 2 700 salariés |
Annualisation du TT |
|
Maintient de 25 emplois permanents |
|
LEFEBVRE 800 salariés |
Annualisation du TT et création de postes (fluctuations saisonnières) |
|
Embauches des - 26 ans en CDI : 20 jeunes en 1994 et 10 en 95 car : implication des cadres, bon climat social, enlacements tenus relatifs à l'emploi |
|
BRIOCHES PASQUIER 1 100 salariés |
Annualiser et aménager le temps de travail en instaurant la semaine de 4 jours, pour :
|
|
|
3. Stratégies offensives privilégiant le temps partiel
3.1. Temps partiel choisi sans compensation versée par l'entreprise
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|
RHONE POULENC CHIMIE 13 000 salaries |
Réduction du coûts et création d'emploi |
Consultation salariés et organisations syndicales PRP par FNE Gestion de la mobilité interne Reconversion avec aides personnalisées |
1 000 a 1 200 mutations internes par an |
|
CARREFOUR 678 salariés concernés Accord renouvelé au bout d'un an |
En réponse aux attentes des salariés
|
|
3.2. Temps partiel avec compensation versée par l'entreprise
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|
FLEURY MICHON 1 900 salariés |
Favoriser ta modulation d'horaires et limiter le chômage des femmes. |
|
|
|
AGF 6 669 salariés |
|
|
Mise en place d'une GRH accompagnée d'une réflexion sur les aménagements du temps de travail possibles. Temps choisi a surtout concerné les femmes salariés. |
|
GROUPE AZUR 2 000 salaries Accord ne concernant que le personnel sédentaire |
|
|
|
|
UAP 9 600 salariés concernes |
Temps choisi, rajeunir la pyramide des âges et accès i l'emploi |
Programmation annuelle
|
4. Modulation du temps de travail et GRH
4.1. des entreprises industrielles
|
Entreprise |
Objectif emploi |
Modalités |
Evolution |
|
UNIMETAL 4 500 salaries |
Temps choisi |
Temps choisi par convention FNE Indemnité de passage au temps partiel Cotisations retraites calculées sur temps plein TRILD < 5 jours sauf volontariat sur 3 mois consécutifs Indemnité complémentaire pour les bas salaires Commission de SUIVI |
|
|
USINOR SACILOR 53 000 salaries |
Préretraite progressive |
PRP par convention FNE
|
4.2. des entreprises de services
|
AFPA 11 000 salariés |
GPEC |
sans avec indemnité forfaitaire de passage.
|
250 embauchés en 1993 450 au premier semestre 94 Prévision de 1 200 départs sur 3 ans. |
|
LA FRANCE ASSURANCE |
GPE |
|
|
|
LA CONCORDE 900 salariés |
Temps partiel et dispense d'activité |
la retraite (60 % salaire brut)
|
|
|
MACIF 5 500 salariés |
PRP pour les + 55 ans |
|
|
|
LES MUTUELLES DE LOIRE ATLANTIQUE 600 salariés |
Création d'emploi et insertion |
PRP avec embauches compensatrices et cotisations retraite sur temps plein Temps choisi sous forme de repos sans solde Développement formation en alternance |
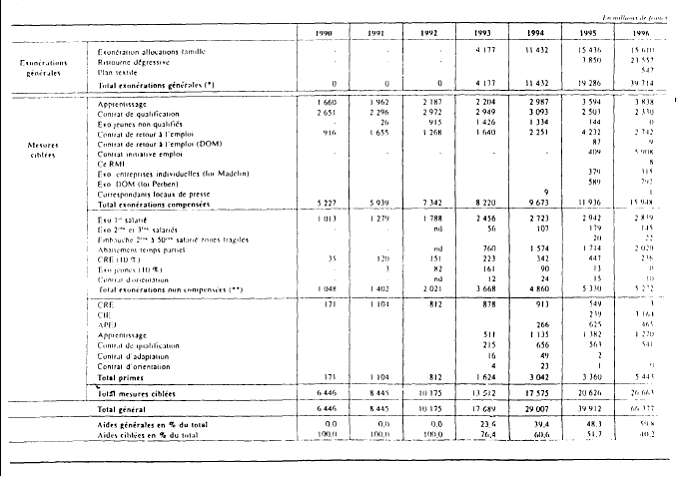
Annexe 2 : Montant financier des mesures
d'allégement du coût du
travail pour l'emploi
marchand
Annexe 3 : Temps partiel contraint ou choisi en France
Actifs à temps partiel « accepté » et à temps partiel « contraint »
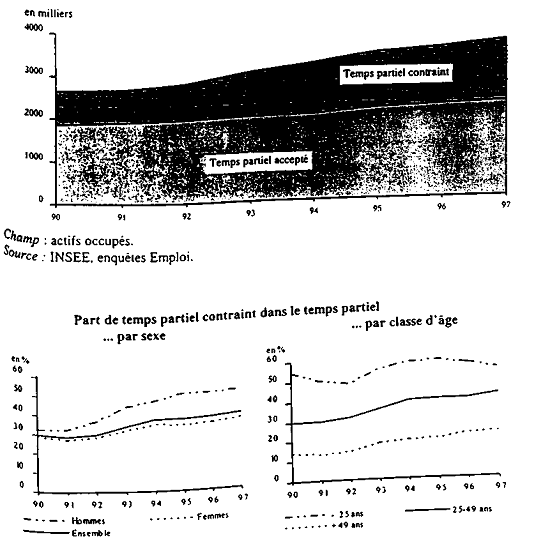
Champ : actifs occupés. Champ : actifs occupés.
Source : INSEE, enquêtes Emploi. Source : INSEE, enquêtes Emploi.
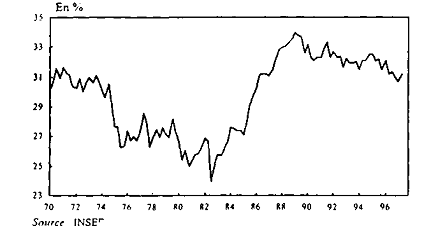
Annexe 4: Taux de marge des sociétés
(Part de l'excédent brut d'exploitation dans la valeur ajoutée)
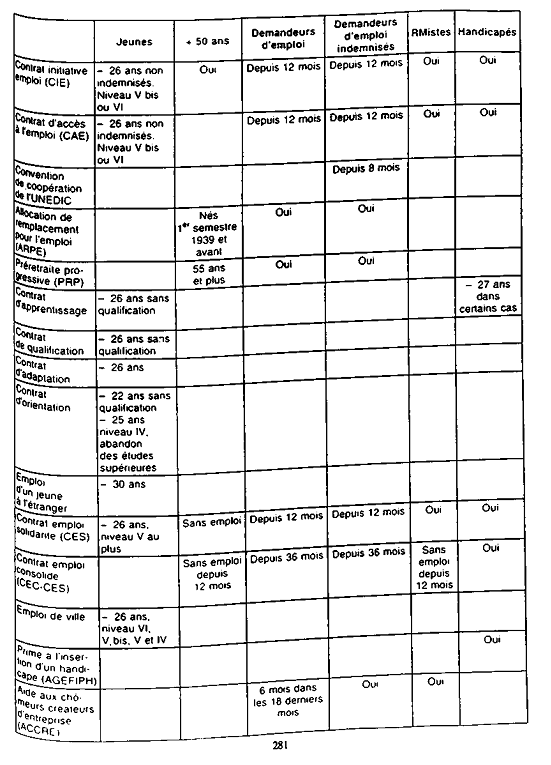
Annexe 5 : Dispositifs ciblés et principaux destinataires
Annexe 6 : Historique des mesures

Annexe 7
ANNEXES MATHÉMATIQUES
|
Le « modèle de Malinvaud » revisité : Les effets d'une baisse des cotisations patronales (Modèle 1) |
Nous nous proposons dans cette annexe mathématique de reprendre le cadre d'analyse présenté par Edmond Malinvaud dans son Rapport du Conseil d'Analyse
Économique de juillet 1998 intitulé « Les Cotisations sociales à la charge des employeurs :
analyse économique » ( confer les pages 77 à 92, « Modélisations visant à préciser
quelques ordres de grandeur » ), pour le compléter par quelques éléments permettant un bouclage complet du modèle que l'auteur a esquissé. Notre attention se portera plus
spécifiquement sur les effets de scénarios alternatifs d'ajustement budgétaire du modèle. Par souci de simplification, nos raisonnements seront tenus en économie fermée.
Nous considérons que la production (notée Q) de l'économie nationale peut être représentée par une fonction de production macroéconomique, à rendements d'échelle constants, combinant deux facteurs de production : du capital et du travail. Cette fonction de production, supposée à facteurs substituables, s'écrit traditionnellement sous la forme d'une Cobb-Douglas, de la manière suivante :

avec 0 <á <1, et où K désigne le stock de capital physique, N le travail, et A la productivité globale des facteurs (c'est-à-dire la technologie) ; t étant un indice de temps.
On considère par ailleurs que l'équilibre comptable de l'économie nationale (en On considère par ailleurs que l'équilibre comptable de l'économie nationale (en économie fermée) permet d'écrire classiquement la production comme :
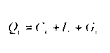
où C représente la consommation. I l'investissement et G les dépenses publiques.
Supposons que la consommation se décompose en une composante de salaires (N) et une composante de revenus non salariaux (R), comme suit :

où < ù > est le taux de salaire réel (hors cotisations sociales), c, et c, étant des paramètres tels que : c 1 + c 2 = 1, avec : 0 < c 1 < 1 et 0 < c 2 < 1.
La dynamique d'accumulation du capital physique, déterminée selon la méthode de l'inventaire permanent, donne l'écriture de l'investissement suivante :
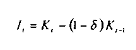
avec < ä > le taux de dépréciation du stock de capital physique, tel que : < ä > 0.
Nous reviendrons plus loin sur les choix d'écritures des dépenses publiques en fonction de leurs modes de financement alternatifs (taxation sur le produit versus cotisations sociales notamment), sur lesquels nous centrerons notre problématique.
Si l'on suppose, par simplification, qu'à long terme, le taux de croissance de l'économie est nul, nous aurons :
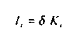
Aussi l'équilibre comptable de la production devient-il dans le long terme, sous sa forme développée :
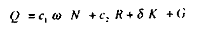
Nous considérons par ailleurs que, dans cette économie, les entreprises cherchent à minimiser intertemporellement leurs coûts de production, selon :
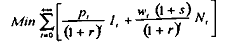
sous la contrainte :
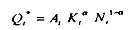
où s désigne le taux de cotisation sociale sur les salaires, p le prix des biens dans l'économie nationale, et r un taux d'actualisation (correspondant au taux d'intérêt nominal). L'exposant * que la variable Q est à considérer ici comme une demande anticipée.
La résolution de ce programme d'optimisation intertemporelle par les entreprises consiste, en utilisant les techniques mathématiques habituelles en la matière, à former le Lagrangien L :
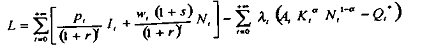
lequel Lagrangien vérifie à l'optimum les conditions de premier ordre suivantes :
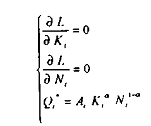
où < ë > est le coefficient multiplicateur On a ainsi :
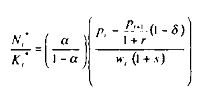
Sur cette base, en réécrivant la fonction de production macroéconomique sous la forme équivalente suivante :
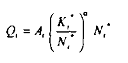
et en posant que le taux d'inflation (ô) de cette économie vaut :
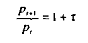
il vient simplement :
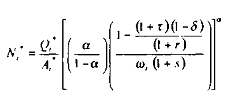
De manière symétrique, en posant :
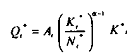
il s'ensuit que :
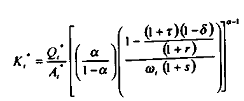
Or, par approximation, on a :
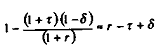
le terme (r-t) correspondant au taux d'intérêt réel. L'expression (r - t + ä) donc au coût d'usage du capital.
Il devient dans ces conditions possible de dériver les équations de demandes de facteurs de production dans le long terme. Nous obtenons par conséquent l'expression de la demande de travail :
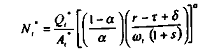
Avec, en dynamique :
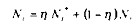
où ç est un paramètre tel que : 0< ç <1.
De même, nous avons l'écriture de la demande de capital suivante :
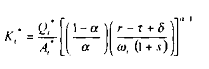
Avec, en dynamique :
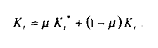
où la valeur paramétrique de ì est telle que o< ì < 1:
Nous reprenons l'équation de salaire proposée par Malinvaud, que l'on peut interpréter comme celle de l'offre de travail :
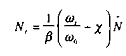
â et ÷ étant des coefficients positifs Le terme « N barre » représente la population disponible à la recherche d'un emploi.
Nous admettrons que les variables anticipées et effectives s'égalisent dans le long terme :
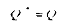
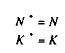
On a alors :
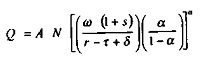
et :
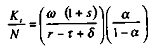
A partir des expressions de la fonction de production d'une part et de l'équilibre comptable de l'économie d'autre part, on obtient la relation suivante :
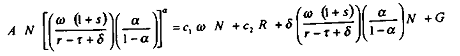
Si maintenant on suppose que les revenus autres que salariaux sont proportionnels au Produit final (î étant un coefficient strictement positif), de sorte que :
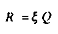
de ce qui précède, il est alors possible de déduire simplement :
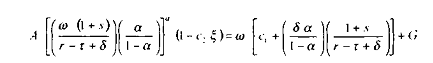
A ce niveau, deux scénarios alternatifs d'ajustement budgétaire sont examinés, selon que les dépenses publiques G sont supposées financées par une taxation sur le produit (hypothèse 1) ou par des cotisations sociales sur les salaires (hypothèse 2).
Hypothèse 1
Supposons que :
G = ø Q
où le taux d'imposition est un paramètre tel que : 0 < < 1.
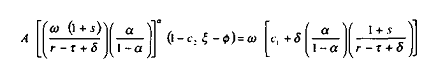
Dans ce premier cas, nous avons :
d'où il vient l'expression du taux de salaire réel :
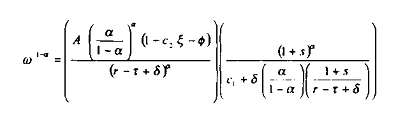
Si ä = 0, alors l'équation précédente peut se réécrire comme :
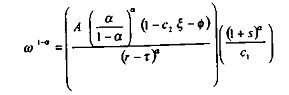
Il apparaît clairement que ù une fonction croissante de s.
Conclusion 1
Toute diminution de s entraîne donc une ù par conséquent une baisse réduction de N. Une diminution du taux des cotisations sociales a dans ces conditions un effet négatif sur l'emploi dans l'économie considérée.
Hypothèse 2
Supposons maintenant que :
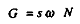
où, comme précédemment indiqué, s est le taux de cotisation sociale et ù le taux de salaire réel.
Dans ce second cas, nous avons :
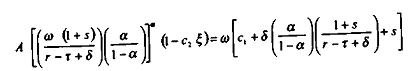
d'où il vient l'expression du taux de salaire réel :
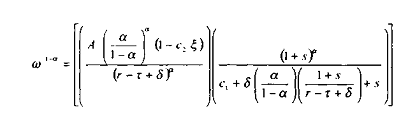
Si ä = 0, alors cette expression de ù devient :
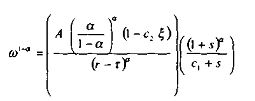
Ici, puisque 0 < á< 1 et 0 < c 1 < 1 , ù devient une fonction décroissante de s.
Conclusion 2
Toute diminution de s entraîne donc une hausse de , et par conséquent augmentation de N. Une diminution du taux des cotisations sociales a dans ces conditions un effet positif sur l'emploi dans l'économie considérée.
|
Le transfert des cotisations sociales
|
Considérons maintenant que, dans l'économie étudiée, les firmes tendent à maximiser intertemporellement leurs profits, selon :
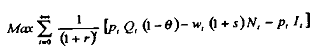
où s désigne toujours le taux de cotisation sociale sur les salaires, è le taux de taxation sur la valeur ajoutée, et r le taux d'intérêt nominal.
Les entreprises sont confrontées au programme d'optimisation suivant :
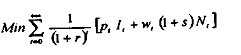
sous la contrainte :
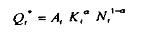
et dont la résolution donne les deux équations de long terme des demandes factorielles (de travail et de capital) suivantes :
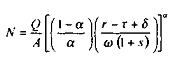
et :
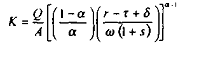
La consommation s'écrit comme la somme des salaires et des autres revenus :
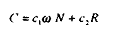
Avec ù le taux de salaire réel (hors cotisations sociales).
L'offre de travail est donnée par :
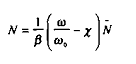
La production en longue période est déduite de l'équilibre comptable de l'économie (en économie fermée), soit :
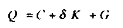
où G sont les dépenses publiques.
Posons des revenus non salariaux proportionnels au produit final, avec î >0 :
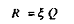
d'où :
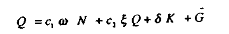
A ce niveau, nous examinons deux scénarios alternatifs d'ajustement budgétaire, selon que les dépenses publiques G sont supposées financées par une taxation sur le produit -- i.e. comptablement, sur la somme des valeurs ajoutées- (hypothèse 1) ou par des recettes provenant à la fois de cotisations sociales sur les salaires et d'une taxe sur la valeur ajoutée (hypothèse 2).
Hypothèse 1
Si l'on suppose que :
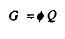
avec un paramètre tel que : 0< < 1, la conclusion précédemment mise en évidence par la résolution du scénario n° 1 dans la présentation du « modèle de Malinvaud » est conservée : ù est fonction croissante de s.
Conclusion 1
Toute diminution de s entraîne donc une réduction de ù, et par conséquent une baisse de N. Une diminution du taux des cotisations sociales a dans ces conditions un effet négatif sur l'emploi dans l'économie considérée.
Hypothèse 2
Supposons à présent que :
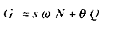
où le terme è s'interprète comme la recette d'une taxe sur la valeur ajoutée, et S ù N comme celle constituée par les cotisations sociales sur les salaires
Dans ce cas, il vient :
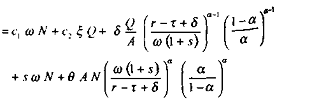
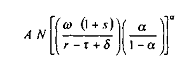
En conséquence, en posant un taux de dépréciation nul du capital, et à niveau de dépenses publiques inchangé, l'expression de la ; de dépréciation nul du capital, et à niveau 1 de la production devient en différenciant :

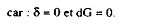
Or, de l'équation de demande de travail, on obtient l'équation suivante :
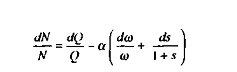
En acceptant la nullité du paramètre ÷ nous dérivons de l'écriture de l'offre de travail ceci :
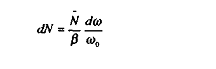
Comme dG = 0, on peut écrire :
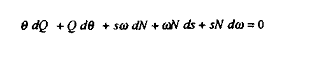
On obtient ainsi :
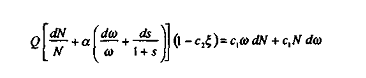
Or :
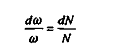
Donc :
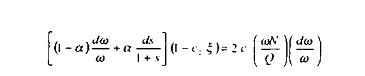
Il vient alors
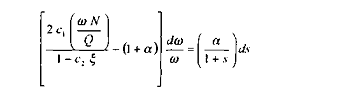
En retenant les valeurs de paramètres suivantes, conformes aux données statistiques disponibles :
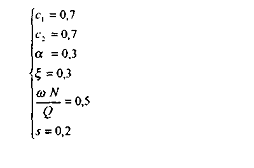
ce calibrage très simple du modèle montre que :
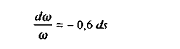
et :
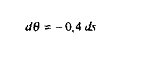
Conclusion 2
Toute diminution de S 2 entraîne donc une hausse de ù et par conséquent une augmentation de N. Une diminution du taux des cotisations sociales a dans ces conditions un effet positif sur l'emploi dans l'économie considérée. Donc, le transfert des cotisations sociales vers une taxe sur la valeur ajoutée est bénéfique pour l'emploi de cette économie, et ce sans détériorer le budget de l'État
|
Le transfert des cotisations sociales
|
Il s'agit maintenant de créer une assiette d'imposition avec une taxe sur l'excédent brut d'exploitation. La question est de savoir si le transfert des charges sociales vers telles taxes a un effet positif sur l'emploi ou non.
Considérons que la firme cherche à résoudre le programme d'optimisation :
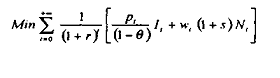
sous la contrainte :
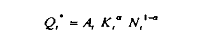
où s est le taux de cotisation sociale sur les salaires, 0 le taux de taxation sur la valeur ajoutée, et r le taux d'intérêt nominal ; avec :
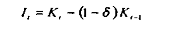
Si l'on pose, pour simplifier les écritures :
alors, dans le long terme, les demandes de facteurs travail et capital sont les suivantes :
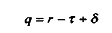
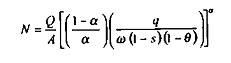
et :
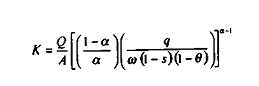
Avec ù le taux de salaire réel (hors cotisations sociales).
Comme précédemment, l'offre de travail est donnée par :
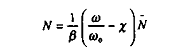
La production s'écrit comme :
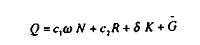
Nous supposerons dans ce qui suit que ä = 0
À ce niveau, nous choisissons d'écrire, dans cette version du modèle, les dépenses publiques comme financées d'une part à partir des cotisations sociales sur salaires. Et d'autre part grâce aux recettes provenant d'une taxe sur l'excédent brut d'exploitation (c'est-à-dire sur une assiette déduisant les salaires des valeurs ajoutées) ; soit :
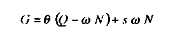
où l'ajustement budgétaire opérera entre è et s de telle manière que les dépenses publiques
demeurent inchangées en niveau (dG = 0).
Ainsi, en différentiant, il vient :
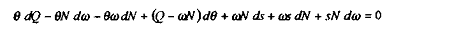
On considère qu'initialement, le paramètre est nul (c'est-à-dire que l'on se retrouve dans le cas de figure précédent où le financement des dépenses publiques n'est couvert que par cotisations sociales sur salaires). En conséquence, on a simplement :
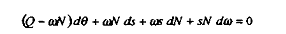
nous avons aussi :
Puisque
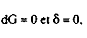
Puisque (dG = 0)
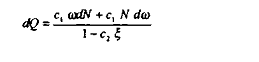
et, par ailleurs, comme, initialement. è = 0
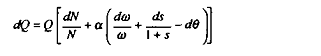
Or, on sait que :
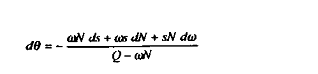
Donc :
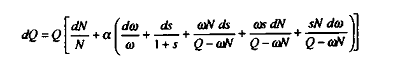
Si ÷ = 0 , alors on a :
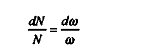
Il vient :
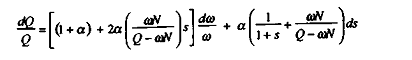
D'où l'on déduit finalement l'expression :
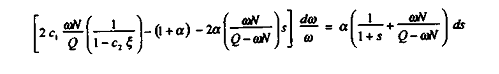
On a :
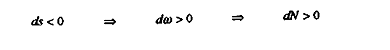
En acceptant les valeurs de paramètres suivantes, selon les données statistiques disponibles :
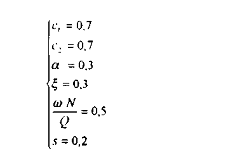
ce calibrage très simple du modèle montre que :
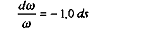
et :
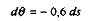
L'impact est donc sensiblement plus fort que dans le modèle avec taxe sur la valeur ajoutée, dans la mesure où le coût relatif du travail diminue davantage dans cette version avec taxe sur l'excédent brut d'exploitation : s diminue et è augmente. L'augmentation de la taxe sur l'excédent brut d'exploitation est plus forte que dans le cas de la taxe sur la valeur ajoutée (car l'assiette d'imposition est plus réduite).
Conclusion
Toute diminution de s entraîne donc une hausse de et par conséquent augmentation de N. Une diminution du taux des cotisations sociales a dans ces conditions un effet positif sur l'emploi dans l'économie considérée. Le transfert des cotisations sociales vers la taxe sur l'excédent brut d'exploitation a un impact positif sur l'emploi de cette économie, sans pour autant détériorer le budget de l'État.
|
La modulation des cotisations sociales
|
Nous considérons maintenant que l'économie est composée de deux firmes indicées 1 et 2, qui se partagent entre elles le marché domestique, selon un paramètre de distribution positif noté ì Ces deux entreprises résolvent un programme d'optimisation identique, prenant la forme de celui présenté précédemment, dans la première version modèle « à la Chadelat ». Ce programme permet de déduire les équations de demande de facteurs de production des entreprises 1 et 2.
et:
Les demandes de facteur travail et de facteur capital dans le long terme pour la firme 1 sont respectivement :
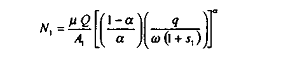
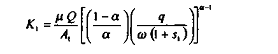
Symétriquement, les demandes factorielles sont pour la firme 2
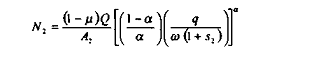
et :
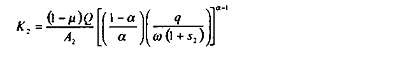
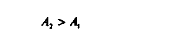
Nous supposons d'une part, qu'initialement, le taux de cotisations sociales sur les salaires est le même dans les deux secteurs :
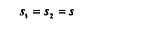
D'autre part, que la proposition de la masse salariale dans la production est plus forte dans le secteur 1 que dans le secteur 2
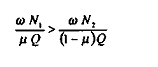
La consommation totale, somme des salaires (versés dans les deux secteurs) et des autres revenus, s'écrit désormais :
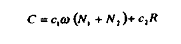
Avec ù le taux de salaire réel (hors cotisations sociales).
L'offre totale de travail est toujours donnée par :
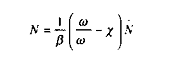
avec :
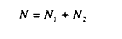
La production totale de l'économie en longue période vaut maintenant :

où G sont les dépenses publiques, et pour un paramètre positif :
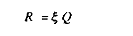
Nous choisissons dans la suite du raisonnement un financement des dépenses publiques G par des recettes provenant des cotisations sociales sur les salaires prélevées dans les deux secteurs ; ce qui s'écrit :
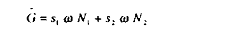
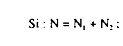
alors :
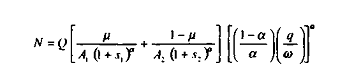
On obtient donc :
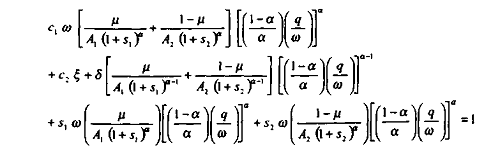
En supposant nul le taux de dépréciation du capital, il vient :
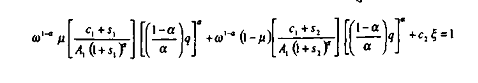
Posons pour simplifier les écritures que :
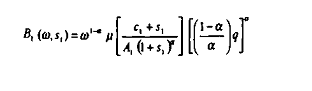
Et
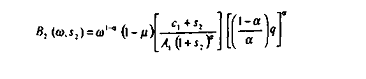
et différentions ces expressions :
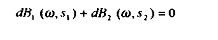
Avec :
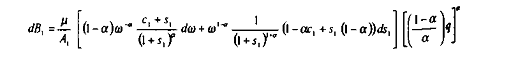
et
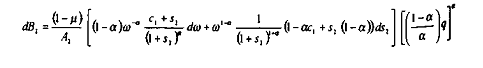
Il vient, par sommation de ces deux dernières expressions, en conservant l'hypothèse de taux de cotisations sociales initialement égaux pour chacune des firmes :
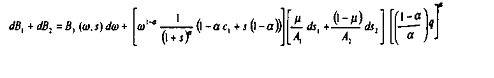
où :
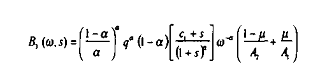
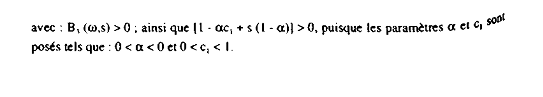
À ce niveau, nous examinons un scénario d'ajustement budgétaire dans lequel les dépenses publiques G sont supposées financées grâce aux cotisations sociales sur les salaires, mais en modifiant la charge respective incombant à chacun des deux secteurs, en faveur du secteur 1 (secteur où la part de la masse salariale dans le produit est relativement plus importante) et en défaveur du secteur 2 (relativement moins « travaillistique »).
On différencie les variations des taux de cotisations sociales selon la règle :
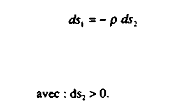
Le paramètre p est proportionnel au contenu en emploi des entreprises. Concrètement, on retient une valeur de ce paramètre telle que :

On trouve :
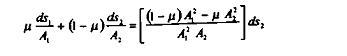

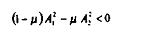
Dans ces conditions, une hausse de S 2 et une baisse de S 1 selon la règle annoncée ci-dessus, entraîne une augmentation de ù et donc aussi de N.
Conclusion
Toute diminution de s 1 , autorisée par un accroissement de s 2 , entraîne donc une hausse de ù et par conséquent une augmentation de N. Une diminution du taux des cotisations sociales dans le secteur où le facteur travail est abondamment utilisé, financée par une augmentation du taux de cotisations sociales dans le secteur où la part de la masse salariale dans la produit est relativement moins importante, a dans ces conditions un effet positif sur l'emploi total dans l'économie considérée.







